Notice: If you have coding experience, I highly recommend to try and solve the puzzle in a language you already know. It's a lot of fun and you'll be able to focus on Go more later on.

We’re one week in! How many puzzles did you solve on your own? Did you solve todays puzzle already? If you haven’t done so yet, go and read the problem description. Go on, I’ll wait here until you’re ready.

Good, you’re back! Let’s get started. On the agenda for today: proper structs and pointers, finally, and recursion!

Structs and pointers

In today’s puzzle involves a number of programs that are linked together to form a tree. Our first task is to find the root program of the tree. Let’s get started by modeling a program with a data structure or struct:

type Program struct {
	name     string     // the name, read from input
	weight   int        // the weight, read from input
	ids      []string   // the ids of child programs, read from input
	children []*Program // references to the other child programs
	root     bool       // indicator to track the root node
}

If that statement looks familiar, it’s because it looks a lot like how we defined the banks type as an []int yesterday. But instead of an []int, we’re now defining Program as a struct with 5 fields. Each of the fields has its own type and they can point to slices of objects of the same type as well. There are a couple of ways to allocate an object of a struct type:

var p1 Program
p2 := Program{}
p3 := Program{"foobar", 42, []string{}, nil, true}
p4 := Program{root: true}

pp1 := &Program{}
pp2 := new(Program)
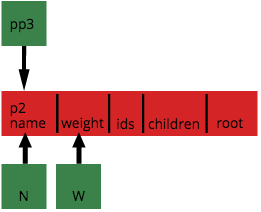
pp3 := &p2

p1 and p2 are Program objects. In each case, the fields are set to their empty values: empty strings, 0 and false for ints and bools, and empty slices. pp1, pp2 and pp3 on the other hand are pointers to Program objects, or *Program. A pointer is a small variable that holds the memory address of an object. While pp1 and pp2 point to anonymous objects, pp3 holds the address of the object p2.

Besides the “empty” struct allocations, there’s also a way to allocate a struct with known values as shown with p3 and p4. This form is called a “composite literal”. If the names of the fields are not specified, like the p3 example, then all the fields have to be specified, in the same order as in the struct definition. When the names are specified, you can leave out the fields that should get their empty values and only specify the fields you actually want to initialize, like root in p4.

In the example above, we referenced (took the address of) the whole Program object. If we want to, we can also get the address of the individual fields like name and weight:

n := &(p2.name)
w := &(p2.weight)

The image below shows you the relation between a Program object p2 and the *Program object pp3 and the pointers to the fields in a more visible way.

Part A: The solution

Now that we know about structs and pointers, let’s get back to the puzzle and parse a input line into a Program object:

func parse(s string) *Program {
	p := Program{root: true}

	ss := strings.Split(s, " -> ")

	_, err := fmt.Sscanf(ss[0], "%s (%d)", &p.name, &p.weight)
	if err != nil {
		panic(err)
	}
	if len(ss) > 1 {
		p.ids = strings.Split(ss[1], ", ")
	}

	return &p
}

A little walkthrough:

• Initialize a Program object, with its root field set to true and assign it to the variable p. Every program is now the root of its own tree.
• Split the input string. The first part will always contain the name and weight, the second part may contain the ids of the child programs.
• Use fmt.Sscanf to parse the name and weight from the first input part, and store it in the corresponding fields of p. Each of the fields must be passed to Sscanf as a pointer. Panic if Sscanf encountered an error.
• If there’s a second part of input, split it into the separate child program ids and assign the slice to the ids field of p.
• Return a pointer to p.

We’ve got our Programs as objects in our code now, time to move on with the actual solution:

func main() {
	if len(os.Args) < 2 {
		fmt.Println("Expected the input file name as commandline argument.")
		os.Exit(1)
	}

	programs := readFile(os.Args[1])

	// Link all the programs together
	for _, p := range programs {
		for _, c := range p.ids {
			programs[c].root = false
			p.children = append(p.children, programs[c])
		}
	}

	var root *Program
	for _, p := range programs {
		if p.root {
			root = p
			break
		}
	}

	fmt.Println("Part A", root.name)

	_, diff := root.Weight()

	fmt.Println("Part B", diff)
}

Some more walking through:

• Take the filename as CLI argument and parse it into a map[string]*Program variable called programs. The name of the programs is used as key in the map.
• Look over the child ids of every program ** Mark all the child programs as “Not a root program”. ** Append the pointer to the child program to the parents children slice
• Loop over all programs to find that one remaining root program
• Call the Weight method of the root program to find the weiht difference diff of the bad node.

Part B: Recurse away

Looks like we have part A all nailed down. But we’re still missing a method called Weight for part B. Well, in the same way we added functions to the banks type yesterday, we can also add a Weight function to the *Program type by adding a receiver to the function definition. The Weight function now has access to all the fields of the receiver object p.

func (p *Program) Weight() (int, int) {
	// Collect the weights of all the child nodes
	weights := []int{}
	for _, c := range p.children {
		w, diff := c.Weight()
		if diff != 0 {
			return 0, diff
		}
		weights = append(weights, w)
	}

	sum := 0
	for idx, i := range weights {
		// Check if this weight matches the other weight
		samevalues := 0
		for _, j := range weights {
			if i == j {
				samevalues++
			}
		}
		// Only matches itself, this is the bad one
		if samevalues == 1 {
			diff := weights[(idx+1)%2] - i
			return 0, p.children[idx].weight + diff
		}
		// Ok, matches, add to the sum
		sum += i
	}

	return sum + p.weight, 0
}

I like walking today, so here we go again for a little walkthough:

• First of all, we’re recursively collecting the weight of the subtrees that are attached to all children. If one of those subtrees returns a non-zero difference, the bad program was in that subtree. We have to return that diff to the caller, which will return the diff to its caller,… all the way to the initial call on the root object in the main function.
• Next we need to check if one of the child nodes is the actual bad node. We compare all weights to all the other weights and if one does not match, we compute the difference and return what the weight field of the child should be.
• If all children have the same weight, we sum them, add the weight of the parent node and return the sum and a 0 difference.

And it’s a wrap! As usual, my full solution is available in my github repository. See you all tomorrow!